ポートフォリオ理論が構築される前の株式投資の損得の予測は大雑把なものでした。「この会社は大きな利益が期待できるけれど、大損もあり得る」または「利益は少ないが、ほぼ損はしないだろう」といった感じです。テクニカル分析やファンダメンタルズ分析は既に存在したものの、”なんとなくそれらしい値段”により株は取引されていたのです。
しかし、株式投資をより科学的に行いたいなら、単に上がった下がっただけでなく、将来的に株価がどの位の上がることが期待できるのか?また損する可能性がある場合はどの位の金額を覚悟するべきかなどが知りたいですね。相場感とかではなく数式を使った定量的な評価を行いたいのです。
ノーベル経済学賞を受賞したハリー・マーコビッツは、株価の平均的な儲けを「リターン」、株価の変動の激しさを「リスク」として、株式投資を数学的に評価する方法を提案しました。彼はリターンとリスクを正規分布によって関連づけて、株価の動きを確率で表現できるようにしたのです。これにより株式投資の収益性を数値で計算できるようになったのです。
リスク、リターン、正規分布
株価はさまざまな要素によって決まります。売上高、景気、ライバル会社の動向などが要因です。これらは複雑に絡み合っているので株価がどれだけ上がるか、下がるかを予想するのは簡単ではありません。1年後に5万円上昇するなどとピタリ言い当てることは難しいですよね。でも、5万円まで上がる確率は60%などといった感じで評価できるのであれば株式投資も数学的に扱えるようになるのです。マーコビッツは、株価の変動を数学的に扱えるように、「リターン」と「リスク」という2つのパラメータだけに絞って株価の未来を評価することにしました。
リターンとリスクを関連付けているのが正規分布です。図1に正規分布のグラフを示します。正規分布はベルのような形でグラフです。正規分布は平均と標準偏差でその特徴を説明できます。後で説明しますが株式投資の場合、平均がリターン、標準偏差がリスクに相当します。平均はベルの中心位置を表しており、標準偏差はベルの太さを示しています。
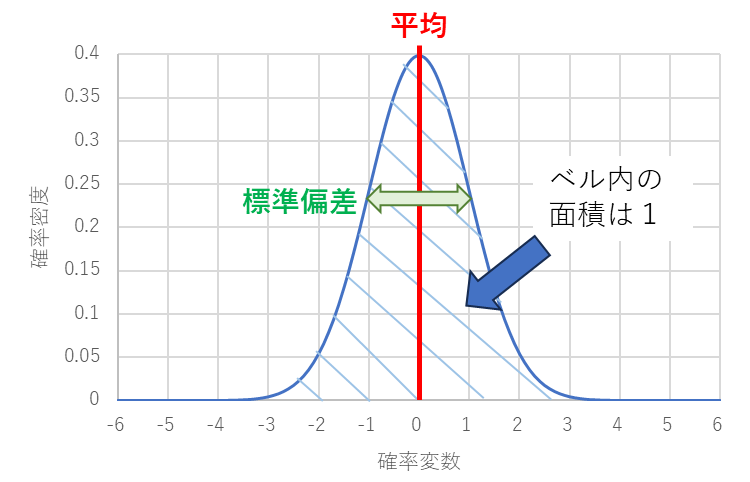
図1の横軸は確率変数と呼ばれるのものですが、簡単に言ってしまえば真ん中である平均(中心)からどれだけずれているかを示す目盛りです。株価で言えば予想株価の平均からどれだけ増えるか、どれだけ減るかを表すものです。一方、縦軸は確率密度と呼ばれています。(単に確率でない理由は最後のメモに書いてありますので興味がある方は読んでください。)実用上は単純に確率と考えても特に問題はないです。
また、正規分布のベル内部の面積(青斜線の部分)は1となります。その理由は正規分布とは確率なので確率変数を-∞~+∞までの確率を足し合わせる(つまり、すべての確率変数の確率を足し合わせる)とその確率は1(100%)になるためです。
この正規分布で株式の値動き変動に利用される場合は、平均がリターン、標準偏差がリスクでした。このリスクとリターンが決定される期間、つまり、どの時点からどの時点までを評価するかの期間は、自由に決められるのですが、ここの説明では1年分のリターンとリスクと定義しておきましょう。この前提のもと、株式投資で使われる正規分布はたとえば図2のように表現されます。平均にリターンが表されて、株価のブレの標準偏差がリスクになります。
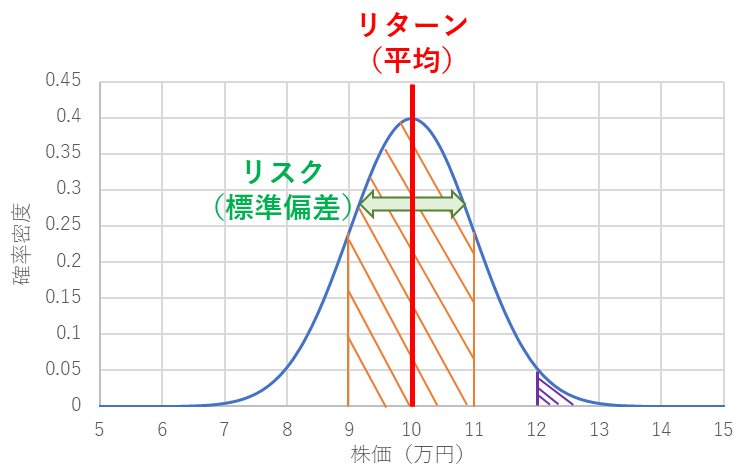
この図2では1年後の株価が9万円~11万円の間になる確率を求めたければ、図2のオレンジ色の網掛けの部分の面積を求めればよく(数学的には積分する)、計算してみると0.7065だったとします。つまり株価が9万円から11万円になる確率は約70.7%ということになります。また、12万円以上になる確率は紫色の網掛けの部分の面積を求めればよく、計算すると0.0255だったとすると約2.6%となります。
この記事の始めでリターンとは平均的な儲けと定義しました。だからリターンはグラフのできるだけ右側にあったほう(大きいほう)が儲かりやすいですね。一方、リスクは株価のブレのことでしたからベルの太さでした。ベルが太くなるほどリスクは高く、細くなるほどリスクは小さいということを示しています。ここで、大抵の人はベル(標準偏差)が細いことを好みます。それは大損する可能性を少しでも小さくしたいと思うからです。実際、リスクが大きいとリターンがそれなりでも負ける可能性のほうが高い投資になることもあります。それは「リスクが大きい投資は損な可能性がある」の項で説明します。
図3はリターンを10%とした場合の、標準偏差30%又は20%としたときの正規分布のグラフです。リスクの大きい標準偏差30%のほうが、ベルが潰れて株価の変動範囲が広がっていることが分かります。つまり、株価はリターン付近になる可能性が標準偏差20%よりも低く、大きく値上がりするか又は大きく値下がりする可能性が高いということです。標準偏差が大きいほどここで説明したようにハイリスクになのです。
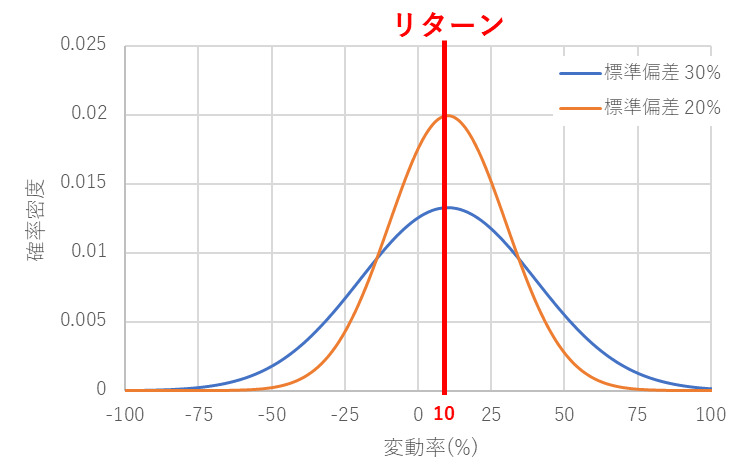
図3の正規分布をみるとリターンから離れていくほど確率が小さくなっていきます。このため正規分布が株価変動を表すのに妥当な表現法と直感的には納得できます。ただ、確率分布には様々な分布や表現があることから、なぜ「正規分布」が使われるのかが疑問に思う方もいるかもしれません。それは後述のコラム1のところで説明します。
正規分布の変動範囲
リスクの大きさを直感的に理解したいですよね。正規分布では68%と95%という数字がよく出てきます。これは変動のブレが標準偏差以内に収まる確率が68%、そして、標準偏差の2倍以内に収まる確率が95%という法則なのです。例えば、リターンがゼロとして標準偏差が10%であれば、株価が±10%以内に収まる確率は68%、2倍の±20%以内に収まる確率は95%ということです。株価が10,000円の場合は、1年後の株価が9,000円から11,000円の範囲内(±10%)となる確率は68%です。8,000円から12,000円の範囲内(±20%)に収まる確率が95%になります。リターンが5%だとした場合は、それぞれ、9,500円から11,500円(±10%)と8,500円~12,500円となります。
べき分布についてはコラム2のファットテールで説明しています。
リスクが大きい投資は損な可能性がある
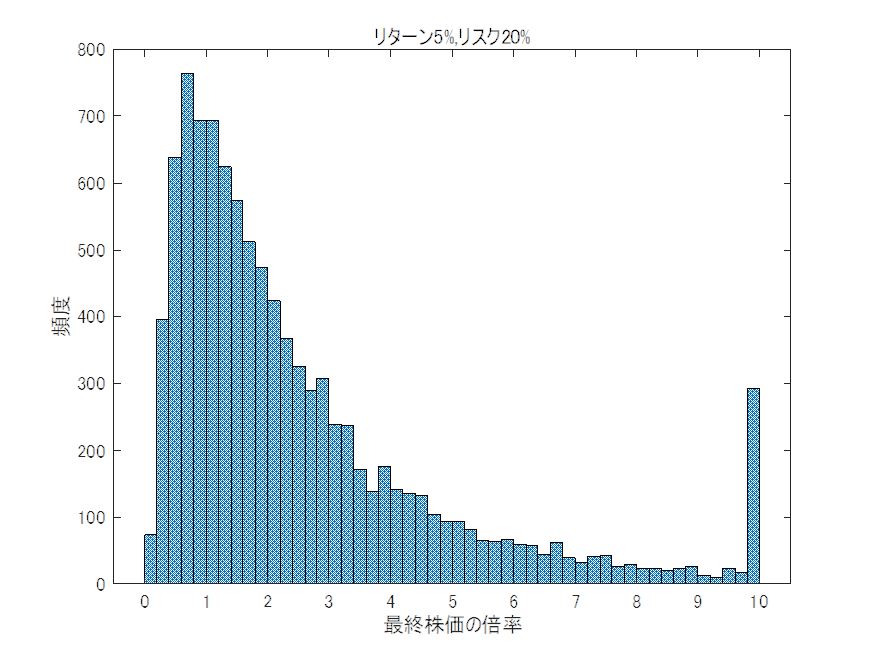
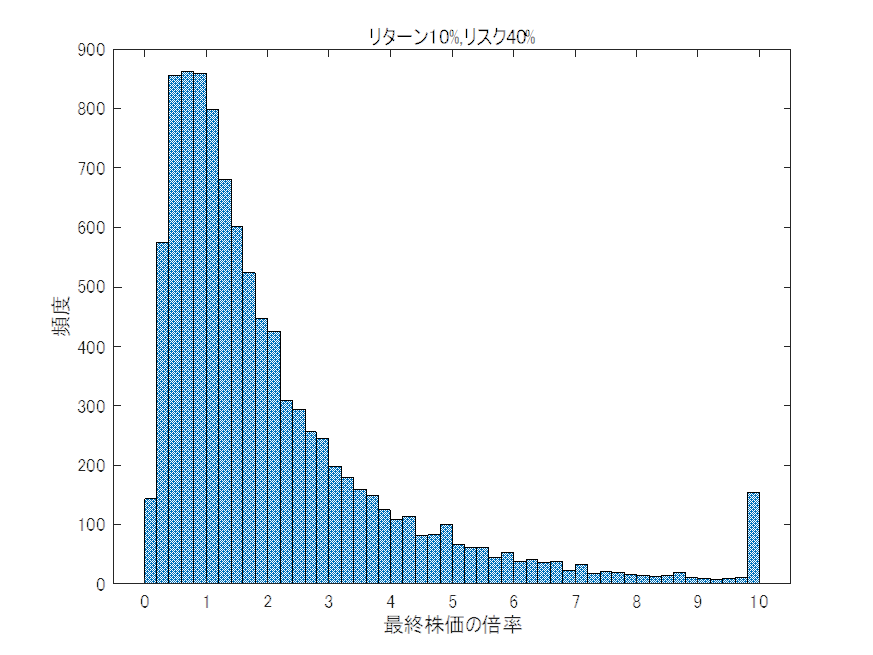
リターンが同じであればリスクはできるだけ小さくしたいものです。ハイリスクでもハイリターンならそれはそれで良いのではないかと思う人もいるかもしれませんが長期投資にはハイリスクは向きません。それを検証するため、図4と図5にシミュレーションを実施しました。(1)リターンが5%でリスクが20%のとき(図4)、(2)リターンが10%でリスクが40%のとき(図5)です。今から20年後の世界を10,000回シミュレーションしてみました。この2つのグラフは20年後の株価がどうなっているのかシミュレーションした結果のヒストグラムです。縦軸については、棒グラフが長いほどそれが発生した回数が多いことを示してます。横軸が1の場合は20年後も株価が変わっていない、2の場合は株価が2倍になったことを示しています。逆に0.5の場合は株価が半分になったことを示しています。縦軸はそれが発生した回数です。全部足すと10,000になります。
(1)では20年後には株価は平均で2.7倍になります。また、1倍を割り込む(マイナスになる)確率は26%でした。一方、(2)のほうは20年後の株価は平均では2.2倍、また、1倍を割り込む確率は33%でした。このようにリターンが高くてもリスクが大きいと思ったより儲けは少ないのです。それどころか損をしてしまう可能性も高まってしまいます。株式投資はリターンだけを見ていては失敗しかねません。リスクを無視する投資は避けたいところです。
リターンとリスクはどのように求めるか
次に、実際のリターンとリスクはどのように求められるのか考えてみましょう。最初に断っておきますが、リターンを求めるのは非常に難しい問題です。過去のリターンは平均的な儲けですので、1年あたりにどの程度儲かっているかを過去に渡って平均を計算すればリターンを求めることができます。例えば、以下のように計算することが可能です。

年毎の増減の平均値(算術平均)を計算すると、
$$リターン=\frac{1}{4}×10\%+\frac{1}{4}×9.1\%+\frac{1}{4}×(-17.5\%)+\frac{1}{4}×10.2\%=4.45\% $$
この計算は単純ですが、株価は複利で増えることを考える必要があり、実際は上式よりももうちょっと複雑な計算をします。
ただ、このリターンは過去のリターンであって未来を保証してくれるわけではないのであくまでも目安と考えておいたほうが無難です。実は未来のリターンの計算はかなり難しいことが分かっています。未来のリターンの求め方を詳しく知りたい方は山崎元さんの記事が分かりやすいと思います。
リスクの標準偏差のほうは過去の価格変動からのブレからある程度正確に計算できます。過去の株価から計算したリスクは概ね未来のリスクと同じと考えても大丈夫です。表1はサンプル数が4年しかないため信頼性がありませんが、例えば20年分位考えればそれなりに正しい値が出てくると思われます。標準偏差の計算式は以下です。
$$標準偏差=\frac{\sum{(年毎の増減-リターン)^2}}{年数}$$
$$標準偏差=\sqrt{分散}$$
この式に表1の値と計算したリターンを代入すると
$$分散=\frac{(10\%-4.45\%)^2+(9.1\%-4.45\%)^2+(-17.5\%-4.45\%)^2+(16.2\%-4.45\%)}{4}=170.09$$
$$標準偏差=\sqrt{170.09}=13.04\%$$
となります。年毎の増減ブレが大きいほど標準偏差が大きく、小さいほど標準偏差が小さくなります。(なお、統計学では不偏分散という考え方があり上式の標準偏差の計算は厳密ではないという断りをいれておきます。)
コラム1 なぜ株価は正規分布で示されるのか? ~中心極限定理~
株価の変動要因は多岐にわたります。個々の要因(為替、景気動向、人口動態、税金、海外状況、流行・・・など)は予測が困難で、それぞれ異なる分布を持っているかもしれません。しかし、これらの要因が多数存在し、それぞれが独立して影響を及ぼす場合、中心極限定理によれば、株価の総合的な動きは正規分布に近づきます。つまり、個々の要因の予測が難しくても、合計としての株価の動きは予測しやすい性質を持つということです。
中心極限定理とは、独立したランダムな変数の合計や平均が、それらの変数の数が多くなるにつれて、正規分布に近づくという統計学の原理です。この理論は、サンプルの数が十分に多ければ、そのサンプルの合計や平均がどのような確率分布に従っていたとしても、近似的に正規分布に従うということを示しています。
中心極限定理の有名な例としては雑音でしょう。たとえば、電子機器内部の熱雑音は無数の電子のランダムな動きによって生じます。これら一つ一つの電子の動きは予測不可能ですが、大量の電子が関与すると、全体としての雑音信号は正規分布に従います。これは外部からの雑音(電線や工場からのノイズ、宇宙からの放射など)にも当てはまります。これら多様な雑音源が重なり合うと、その合成雑音信号は正規分布に従うことが多いのです。
コラム2 だけど、株価は本当に正規分布で表現できるのか? ~ファットテール~
コラム1でお話したように、従来、株価の動きは正規分布に従うと考えられていました。正規分布は、中心に近い値が最も多く発生し、極端に高い値や低い値は稀にしか現れないという特徴があります。これは、水中でランダムに動く花粉のような動きを表し、株価も同様に予測可能な範囲内で変動するとされていました。
しかし、最近の研究では、株価の動きが実際にはべき分布に従う可能性が高いという考えが広がっています。べき分布は、正規分布とは異なり、極端な値(非常に高い値や低い値)の発生確率が比較的高いことが特徴です。これは、市場の過熱や冷え込みが極端な株価変動を引き起こすことを反映しています。
市場が動揺している場合、例えば大きなニュース(技術革新、コロナショック)が起こったとき、株価は通常よりも激しく変動しやすくなります。これは、水温が上昇した状態での花粉の動きに例えることができます。反対に、市場が閑散としている場合、株価の変動は小さくなります。このような極端な価格変動の可能性が、べき分布における「ファットテール」として現れるのです。
べき分布は、正規分布よりも極端な価格変動をよりよく捉えることができると考えられており、株式市場の実際の挙動をより正確に表すモデルとされています。市場の動きは単純な正規分布で捉えるよりも複雑であるため、投資を行う際は、このべき分布の特性を頭に入れておきましょう。正規分布だけを考えていると足元をすくわます。
メモ 確率密度について
正規分布のグラフにおいて、横軸が「確率」ではなくて「確率密度」となっているのは、このグラフではある一点の確率は計算できないからです。なぜ確率ではないのかというと、正規分布のグラフでは「ある特定の点での確率」は直接計算することができないからです。
例を挙げて説明しましょう。確率変数がちょうど1である場合を考えます。このとき、確率変数が「正確に1.0000000000…」となる確率を求めようとすると、問題が生じます。なぜなら、横軸上でこの値は「幅を持たない点」として表されるため、その点での確率は実質的にゼロとなってしまうのです。正規分布では、確率は「範囲」を使って考える必要があります。たとえば、0.99から1.01の間といった具体的な範囲で考えるのです。このように、確率変数の「範囲」に基づいて確率を考えるとき、その範囲に含まれる確率の総量を計算することができます。













